

__Bayesian Networks in__ __Educational Assessment__
__Session IV:__ __ __ __Refining__ __ __ __Bayes Net with Data__
Estimating Parameters with MCMC
Russell Almond\, FSU
Duanli Yan\, Diego Zapata\, ETS
2021 NCME Tutorial: Bayesian Networks in Educational Assessment
_SESSION_ __ __ _TOPIC_ __ __ _PRESENTERS_
__Session 1__ : Evidence Centered Design Diego Zapata Bayesian Networks
__Session 2__ : Bayes Net Applications Duanli Yan & ACED: ECD in Action Russell Almond
__Session 3__ : Bayes Nets with R Russell Almond & Duanli Yan
__Session 4__ : Refining Bayes Nets with Duanli Yan & Data Russell Almond
Bayesian Inference: Expanding Our Context
# Posterior Distribution
Posterior distribution for _unknowns_ given _knowns_ _ _ is
Inference about examinee latent variables \( _θ_ \) given observables \( __x__ \)
Example: ACED Bayes Net Fragment for _Common Ratio_
_θ_ _ _ = _Common Ratio _
__x__ _ _ = Observables from tasks that measure _Common Ratio _
# Bayes Net Fragment
_θ_ _ _ = _Common Ratio _
_x_ s _ _ = Observables from tasks that measure _Common Ratio _
# Probability Distribution for the Latent Variable
_θ_ _ _ = _Common Ratio _
_θ_ _ ~ _ Categorical\( __λ__ \)
ACED Example
2 Levels of _θ_ \(Low\, High\)
__λ__ = \( _λ_ 1 \, _λ_ 2 \) contains probabilities for Low and High
| | θ (Common Ratio) | |
| :-: | :-: | :-: |
| | 1 | 2 |
| Prob. | λ1 | λ2 |
# Probability Distribution for the Observables
_x_ s _ _ = Observables from tasks that measure _Common Ratio _
\( _x_ _j_ | _θ_ = _c_ \) ~ Bernoulli\( _π_ _cj_ \)
ACED Example
_π_ _cj_ _ _ is the probability of correct response on task _j_ given _θ_ = _c_
| | p(xj | θ) | |
| :-: | :-: | :-: |
| θ | 0 | 1 |
| 1 | 1 – π1j | π1j |
| 2 | 1 – π2j | π2j |
# Bayesian Inference
| | θ (Common Ratio) | |
| :-: | :-: | :-: |
| | 1 | 2 |
| Prob. | λ1 | λ2 |
| | p(xj | θ) | |
| :-: | :-: | :-: |
| θ | 0 | 1 |
| 1 | 1 – π1j | π1j |
| 2 | 1 – π2j | π2j |
If the _λ_ s and _π_ s are unknown\, they become subject to posterior inference too
| | p(xj | θ) | |
| :-: | :-: | :-: |
| θ | 0 | 1 |
| 1 | 1 – π1j | π1j |
| 2 | 1 – π2j | π2j |
A convenient choice for prior distribution is the beta distribution
ACED Example: _π_ 1 _j_ ~ Beta\(1\, 1\) _π_ 2 _j_ ~ Beta\(1\, 1\)
For first task\, constrain \( _π_ 21 > _π_ 11\) to resolve indeterminacy in the latent variable and avoid label switching
| | θ (Common Ratio) | |
| :-: | :-: | :-: |
| | 1 (Low) | 2 (High) |
| Prob. | λ1 | λ2 |
A convenient choice for the prior distribution is the Dirichlet distribution
which generalizes the Beta distribution to the case of multiple categories
ACED Example: λ = \( _λ_ 1\, _λ_ 2\) ~ Dirichlet\(1\, 1\)
λ _~ _ Dirichlet\(αλ\)
# Model Summary
_θ_ _i_ _ ~ _ Categorical\( λ \)
λ ~ Dirichlet \( 1\, 1 \)
\( _x_ _ij_ | _θ_ _i_ = _c_ \) ~ Bernoulli\( _π_ _cj_ \)
_π_ 11 ~ Beta\( 1\, 1 \)
_π_ 21 ~ Beta\( 1\, 1 \) _I_ \( _π_ 21 > _π_ 11 \)
_π_ _cj_ ~ Beta\( 1\, 1 \) for others obs\.
# JAGS Code
for \( i in 1:n\)\{
for\(j in 1:J\)\{
x\[ i\,j \] ~ dbern \(pi\[theta\[ i \]\,j\]\)
\}
\}
\( _x_ _ij_ | _θ_ _i_ = _c_ \) ~ Bernoulli\( _π_ _cj_ \)
| | p(xj | θ) | |
| :-: | :-: | :-: |
| θ | 0 | 1 |
| 1 | 1 – π1j | π1j |
| 2 | 1 – π2j | π2j |
Referencing the table for _π_ _j_ s in terms of _θ_ = 1 or 2
_π_ 11 ~ Beta\( 1\, 1 \)
pi\[1\,1\] ~ dbeta \(1\,1\)
pi\[2\,1\] ~ dbeta \(1\,1\) T\(pi\[1\,1\]\, \)
for\(c in 1:C\)\{
for\(j in 2:J\)\{
pi\[ c\,j \] ~ dbeta \(1\,1\)
\}
\}
_π_ 21 ~ Beta\( 1\, 1 \) _I_ \( _π_ 21 > _π_ 11 \)
_π_ _cj_ ~ Beta\( 1\, 1 \) for remaining observables
for \( i in 1:n\)\{
theta\[ i \] ~ dcat \(lambda\[\]\)
\}
_θ_ _i_ _ ~ _ Categorical\( λ \)
lambda\[1:C\] ~ ddirch \( alpha\_lambda \[\]\)
for\(c in 1:C\)\{
alpha\_lambda \[c\] <\- 1
\}
λ ~ Dirichlet \( 1\, 1 \)
Markov Chain Monte Carlo
# Estimation in Bayesian Modeling
* Our “answer” is a posterior distribution
* All parameters treated as random\, not fixed
* Contrasts with frequentist approaches to inference\, estimation
* Parameters are fixed\, so estimation comes to finding the single best value
* “Best” here in terms of a criterion \(ML\, LS\, etc\.\)
* Peak of a mountain vs\. mapping the entire terrain of peaks\, valleys\, and plateaus \(of a landscape\)
# What’s In a Name?
* Markov chain _Monte Carlo_
* Construct a sampling algorithm to _simulate _ or _draw from _ the posterior\.
* Collect many such draws\, which serve to empirically approximate the posterior distribution\, and can be used to empirical approximate summary statistics\.
* Monte Carlo Principle:
* Anything we want to know about a random variable _θ_ _ _ can be learned by sampling many times from _f_ \( _θ_ \)\, the density of _θ_ \.
* \-\- Jackman \(2009\)
Markov _chain _ Monte Carlo
Values really generated as a sequence or chain
_t _ denotes the step in the chain
_θ_ \(0\)\, _θ_ \(1\)\, _θ_ \(2\)\,…\, _θ_ \( _t_ \)\,…\, _θ_ \( _T_ \)
Also thought of as a time indicator
_Markov _ chain _ _ Monte Carlo
Follows the Markov property…
# The Markov Property
* Current state depends on previous position
* Examples: weather\, checkers\, baseball counts & scoring
* Next state conditionally independent of past\, given the present
* Akin to a full mediation model
* _p_ \( _θ_ \( _t_ \+1\) | _θ_ \( _t_ \)\, _ _ _θ_ \( _t_ \-1\)\, _ _ _θ_ \( _t_ \-2\) \,…\) = _p_ \( _θ_ \( _t_ \+1\) | _θ_ \( _t_ \)\)
# Visualizing the Chain: Trace Plot
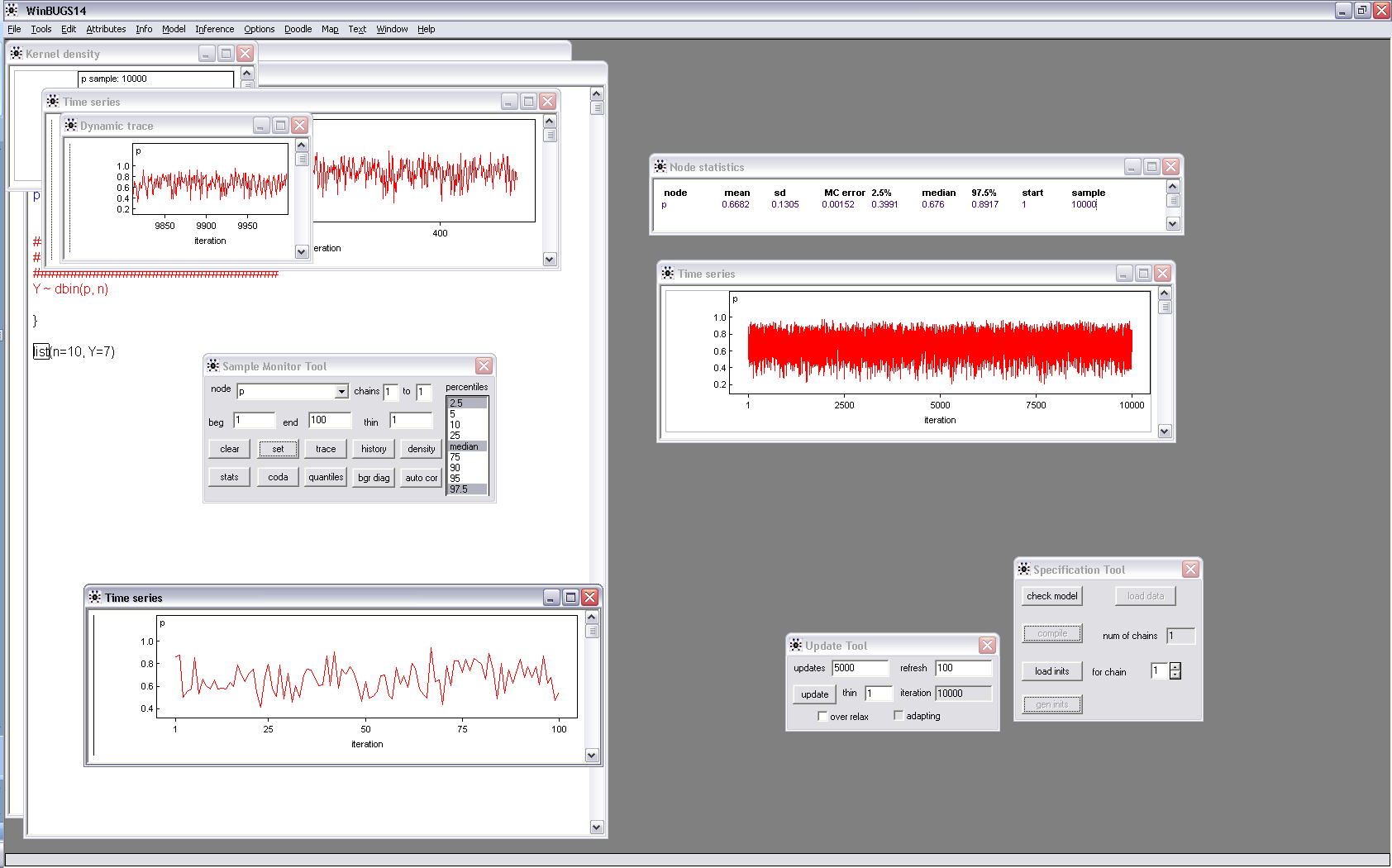
# Markov Chain Monte Carlo
* Markov chains are _sequences of numbers _ that have the Markov property
* Draws in cycle _t\+_ 1 depend on values from cycle _t_ \, but given those not on previous cycles \(Markov property\)
* Under certain assumptions Markov chains reach _stationarity_
* The collection of values converges to a distribution\, referred to as a stationary distribution
* Memoryless: It will “forget” where it starts
* Start anywhere\, will reach stationarity if regularity conditions hold
* For Bayes\, set it up so that this is the posterior distribution
* Upon convergence\, samples from the chain approximate the stationary \(posterior\) distribution
Assessing Convergence
# Diagnosing Convergence
* With MCMC\, convergence to a _distribution_ \, not a point
* ML:
* Convergence is when we’ve reached the highest point in the likelihood\,
* The highest peak of the mountain
* MCMC:
* Convergence when we’re sampling values from the correct distribution\,
* We are mapping the entire terrain accurately
A properly constructed Markov chain is guaranteed to converge to the stationary \(posterior\) distribution…eventually
Upon convergence\, it will sample over the full support of the stationary \(posterior\) distribution…over an ∞ number of draws
In a finite chain\, no guarantee that the chain has converged or is sampling through the full support of the stationary \(posterior\) distribution
Many ways to diagnose convergence
Whole software packages dedicated to just assessing convergence of chains \(e\.g\.\, R packages ‘coda’ and ‘boa’\)
# Gelman & Rubin’s (1992) �Potential Scale Reduction Factor (PSRF)
Run _multiple _ chains from dispersed starting points
Suggest convergence when the chains come together
If they all go to the same place\, it’s probably the stationary distribution
An analysis of variance type argument
_PSRF _ or _R =_
If there is substantial between\-chain variance\, will be >> 1
Run _multiple _ chains from dispersed starting points
Suggest convergence when the chains come together
Operationalized in terms of partitioning variability
Run multiple chains for 2 _T _ iterations\, discard first half
Examine between and within chain variability
Various versions\, modifications suggested over time
# Potential Scale Reduction Factor (PSRF)
For any _θ_ \, for any chain _c_ the within\-chain variance is
For all chains\, the pooled within\-chain variance is
The between\-chain variance is
The estimated variance is
The potential scale reduction factor is
If close to 1 \(e\.g\.\, < 1\.1\) for all parameters\, can conclude convergence
Examine it over “time”\, look for \, stability of _B_ and _W_
If close to 1 \(e\.g\.\, < 1\.2\, or < 1\.1\) can conclude convergence
# Assessing Convergence: No Guarantees
* Multiple chains coming together does not guarantee they have converged
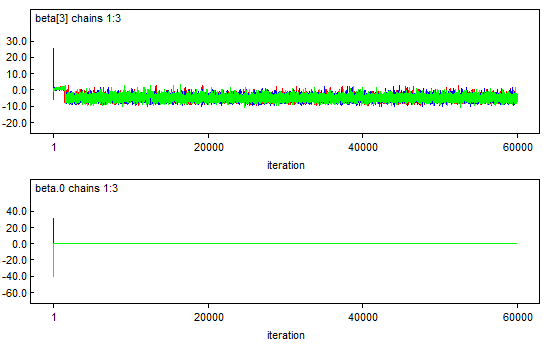
* multiple chains come together does not guarantee they have converged
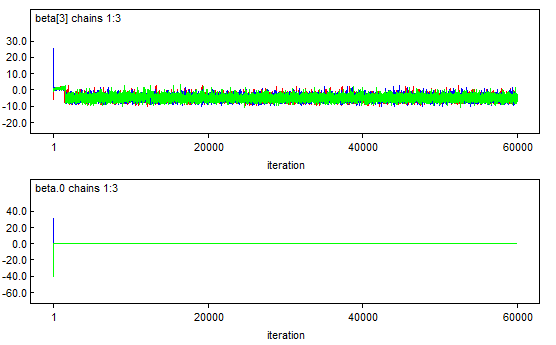
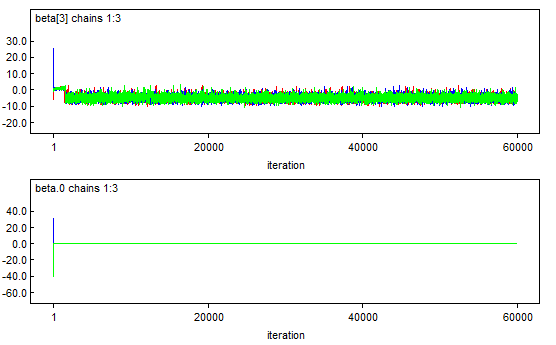

* Multiple chains coming together does not guarantee they have converged
# Assessing Convergence
* Recommend running multiple chains far apart and determine when they reach the same “place”
* PSRF criterion an approximation to this
* Akin to starting ML from different start values and seeing if they reach the same maximum
* Here\, convergence to a distribution\, not a point
* A chain hasn’t converged until _all _ parameters converged
* Brooks & Gelman multivariate PSRF
Serial Dependence
# Serial Dependence
Serial dependence between draws due to the dependent nature of the draws \(i\.e\.\, the Markov structure\)
_p_ \( _θ_ \( _t_ \+1\) | _θ_ \( _t_ \)\, _ _ _θ_ \( _t_ \-1\)\, _ _ _θ_ \( _t_ \-2\) \,…\) = _p_ \( _θ_ \( _t_ \+1\) | _θ_ \( _t_ \)\)
However there is a _marginal _ dependence across multiple lags
Can examine the autocorrelation across different lags
# Autocorrelation
# Thinning
Can “thin” the chain by dropping certain iterations
Thin = 1 keep every iteration
Thin = 2 keep every other iteration \(1\, 3\, 5\,…\)
Thin = 5 keep every 5th iteration \(1\, 6\, 11\,…\)
Thin = 10 keep every 10th iteration \(1\, 11\, 21\,…\)
Thin = 100 keep every 100th iteration \(1\, 101\, 201\,…\)
* Can “thin” the chain by dropping certain iterations
* Thin = 1 keep every iteration
* Thin = 2 keep every other iteration \(1\, 3\, 5\,…\)
* Thin = 5 keep every 5th iteration \(1\, 6\, 11\,…\)
* Thin = 10 keep every 10th iteration \(1\, 11\, 21\,…\)
* Thin = 100 keep every 100th iteration \(1\, 101\, 201\,…\)
* Thinning _does not _ provide a better portrait of the posterior
* A loss of information
* May want to keep\, and account for time\-series dependence
* Useful when data storage\, other computations an issue
* _I want 1000 iterations\, rather have 1000 approximately independent iterations_
* Dependence _within _ chains\, but none _between _ chains
# Mixing
We don’t want the sampler to get “stuck” in some region of the posterior \, or ignore a certain area of the posterior
Mixing refers to the chain “moving” throughout the support of the distribution in a reasonable way
relatively poor mixing
relatively good mixing
* Mixing ≠ convergence\, but better mixing usually leads to faster convergence
* Mixing ≠ autocorrelation\, but better mixing usually goes with lower autocorrelation \(and cross\-correlations between parameters\)
* With better mixing\, then for a given number of MCMC iterations\, get more information about the posterior
* Ideal scenario is independent draws from the posterior
* With worse mixing\, need more iterations to \(a\) achieve convergence and \(b\) achieve a desired level of precision for the summary statistics of the posterior
Chains may mix differently at different times
Often indicative of an adaptive MCMC algorithm
relatively poor mixing
relatively good mixing
* Slow mixing can also be caused by high dependence between parameters
* Example: multicollinearity
* Reparameterizing the model can improve mixing
* Example: centering predictors in regression
Stopping the Chain\(s\)
# When to Stop The Chain(s)
* Discard the iterations prior to convergence as _burn\-in_
* How many more iterations to run?
* As many as you want
* As many as time provides
* Autocorrelaion complicates things
* Software may provide the “MC error”
* Estimate of the sampling variability of the sample mean
* Sample here is the sample of iterations
* Accounts for the dependence between iterations
* Guideline is to go at least until MC error is less than 5% of the posterior standard deviation
* Effective sample size
* Approximation of how many independent samples we have
Steps in MCMC in Practice
# Steps in MCMC (1)
* Setup MCMC using any of a number of algorithms
* Program yourself \(have fun \)
* Use existing software \(BUGS\, JAGS\)
* Diagnose convergence
* Monitor trace plots\, PSRF criteria
* Discard iterations prior to convergence as _burn\-in_
* Software may indicate a minimum number of iterations needed
* A lower bound
# Adapting MCMC Automatic Discard
relatively poor mixing during adaptive phase
relatively good mixing
after adaptive phase
# Steps in MCMC (2)
* Run the chain for a desired number of iterations
* Understanding serial dependence/autocorrelation
* Understanding mixing
* Summarize results
* Monte Carlo principle
* Densities
* Summary statistics
# Model Summary
_θ_ _i_ _ ~ _ Categorical\( λ \)
λ ~ Dirichlet \( 1\, 1 \)
\( _x_ _ij_ | _θ_ _i_ = _c_ \) ~ Bernoulli\( _π_ _cj_ \)
_π_ 11 ~ Beta\( 1\, 1 \)
_π_ 21 ~ Beta\( 1\, 1 \) _I_ \( _π_ 21 > _π_ 11 \)
_π_ _cj_ ~ Beta\( 1\, 1 \) for others obs\.
ACED Example
See ‘ACED Analysis\.R’ for Running the analysis in R
See Following Slides for Select Results
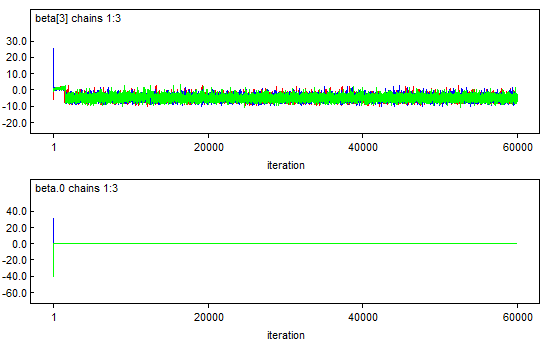
# Convergence Assessment (1)
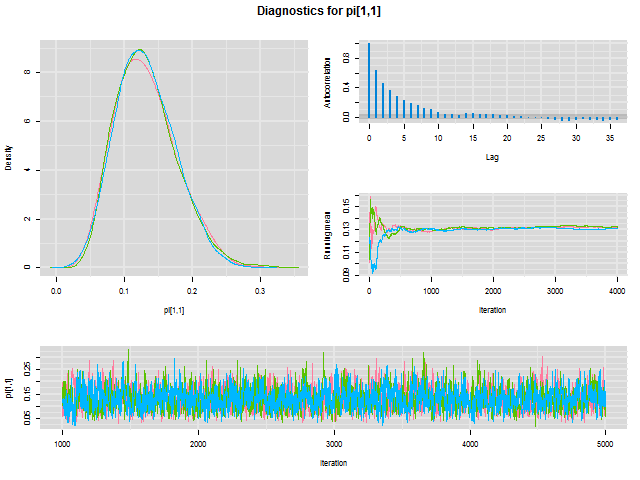
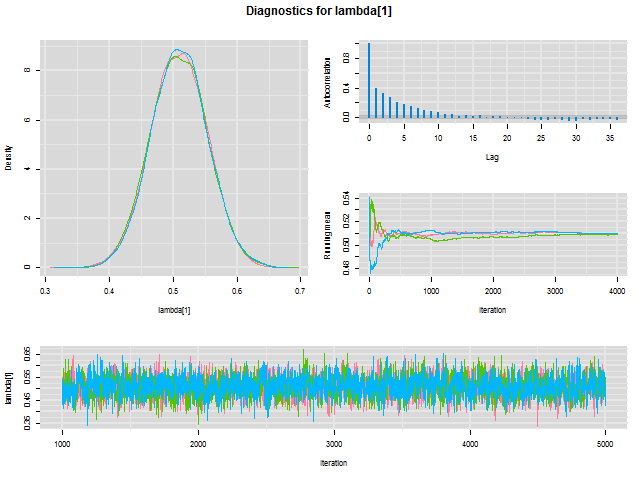
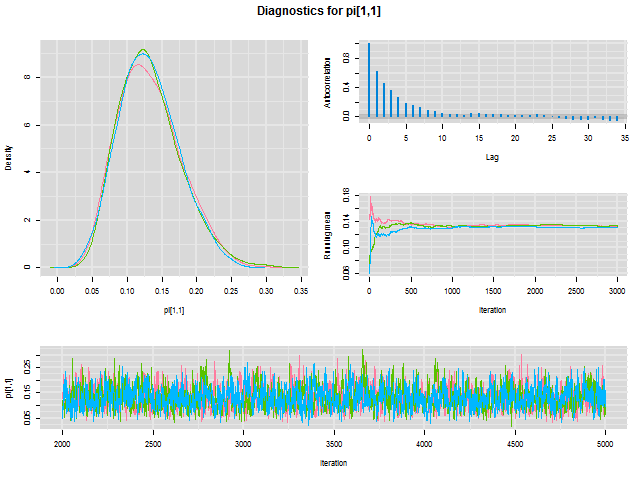
# Posterior Summary (1)
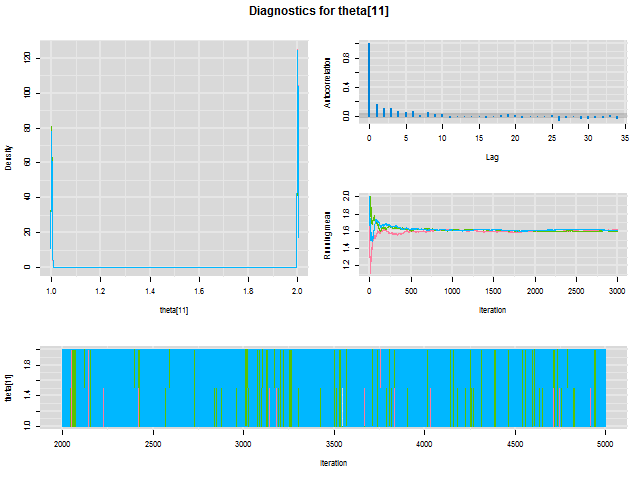
| | Mean | SD | Naive SE | Time-series SE | 0.025 | 0.25 | 0.5 | 0.75 | 0.975 | Median | 95% HPD lower | 95% HPD Upper |
| :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: |
| lambda[1] | 0.51 | 0.04 | 0 | 0 | 0.42 | 0.48 | 0.51 | 0.54 | 0.6 | 0.51 | 0.43 | 0.6 |
| lambda[2] | 0.49 | 0.04 | 0 | 0 | 0.4 | 0.46 | 0.49 | 0.52 | 0.58 | 0.49 | 0.4 | 0.57 |
| pi[1,1] | 0.13 | 0.04 | 0 | 0 | 0.06 | 0.1 | 0.13 | 0.16 | 0.23 | 0.13 | 0.05 | 0.22 |
| pi[2,1] | 0.84 | 0.04 | 0 | 0 | 0.75 | 0.81 | 0.84 | 0.87 | 0.91 | 0.84 | 0.75 | 0.92 |
| pi[1,2] | 0.22 | 0.05 | 0 | 0 | 0.12 | 0.18 | 0.22 | 0.26 | 0.33 | 0.22 | 0.12 | 0.33 |
| pi[2,2] | 0.98 | 0.02 | 0 | 0 | 0.93 | 0.97 | 0.99 | 0.99 | 1 | 0.99 | 0.94 | 1 |
| pi[1,3] | 0.02 | 0.01 | 0 | 0 | 0 | 0.01 | 0.02 | 0.03 | 0.06 | 0.02 | 0 | 0.05 |
| pi[2,3] | 0.19 | 0.04 | 0 | 0 | 0.12 | 0.17 | 0.19 | 0.22 | 0.28 | 0.19 | 0.12 | 0.27 |
| pi[1,4] | 0.03 | 0.02 | 0 | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.07 | 0.03 | 0 | 0.06 |
| pi[2,4] | 0.23 | 0.05 | 0 | 0 | 0.15 | 0.2 | 0.23 | 0.26 | 0.33 | 0.23 | 0.15 | 0.33 |
| pi[1,5] | 0.15 | 0.04 | 0 | 0 | 0.08 | 0.12 | 0.15 | 0.17 | 0.22 | 0.15 | 0.08 | 0.22 |
| pi[2,5] | 0.64 | 0.05 | 0 | 0 | 0.53 | 0.6 | 0.64 | 0.67 | 0.74 | 0.64 | 0.53 | 0.74 |
| pi[1,6] | 0.17 | 0.04 | 0 | 0 | 0.1 | 0.14 | 0.17 | 0.2 | 0.25 | 0.17 | 0.1 | 0.25 |
| pi[2,6] | 0.82 | 0.05 | 0 | 0 | 0.72 | 0.79 | 0.82 | 0.86 | 0.92 | 0.82 | 0.73 | 0.92 |
| theta[1] | 2 | 0.06 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| theta[2] | 1 | 0.02 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| theta[3] | 1 | 0.01 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| theta[4] | 1.97 | 0.17 | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| theta[5] | 1.17 | 0.38 | 0 | 0.01 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 |
| theta[6] | 1 | 0.01 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| theta[7] | 1.01 | 0.07 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Summary and Conclusion
# Summary
* Dependence on initial values is “forgotten” after a sufficiently long run of the chain \(memoryless\)
* Convergence to a _distribution_
* Recommend monitoring multiple chains
* PSRF as approximation
* Let the chain “burn\-in”
* Discard draws prior to convergence
* Retain the remaining draws as draws from the posterior
* Dependence across draws induce autocorrelations
* Can thin if desired
* Dependence across draws within and between parameters can slow mixing
* Reparameterizing may help
# Wise Words of Caution
* Beware: MCMC sampling can be dangerous\!
* \-\- Spiegelhalter\, Thomas\, Best\, & Lunn \(2007\)
* \(WinBUGS User Manual\)