

__Bayesian Networks in__ __Educational Assessment__
__Tutorial__
__Session III: __ __Bayes Net with R__
Duanli Yan\, Diego Zapata\, ETS
Russell Almond\, FSU
2021 NCME Tutorial: Bayesian Networks in Educational Assessment
_SESSION_ __ __ __ __ _TOPIC_ __ __ __ __ __ __ __ __ __ __ __ __ __ __ _PRESENTERS_
__Session 1__ : Evidence Centered Design Diego Zapata Bayesian Networks
__Session 2__ : Bayes Net Applications Duanli Yan & ACED: ECD in Action Russell Almond
__Session 3__ : Bayes Nets with R Russell Almond & Duanli Yan
__Session 4__ : Refining Bayes Nets with Duanli Yan & Data Russell Almond
# Discrete Partial Credit Model: A generic framework for building CPTs
# Russell Almond
# Conditional Probability Tables
* Focus on a child variable
* Child has zero or more parent variables in graph
* For each configuration of parent variables\, need conditional probability of each child variable\.
* Unconditional probability in the case of no parents
* If there are _N_ parents\, each with _M_ states and the child variable has _K_ states\, then the number of unconstrained entries in the table is
* _M_ _N_ _\(K\-1\)_
# Problems
Too many parameters to comfortably elicit
Certain cases might be rare in population \( Very High on _Skill 1_ and Very Low on _Skill 2_ \)
Want to capture intuition of experts on how skills interact to generate performace\.
# Reduced Parameter Models
* Noisy\-and and Noisy\-Or models
* NIDA\, DINA and Fusion model \(Junker & Sijtsma\)
* Assume binary responses
* Discrete IRT models
* DiBello—Samejima models
* Based on “effective theta” and graded response model
* Compensatory\, Conjunctive\, Disjunctive and Inhibitor relationships
* CPTtools framework
* Effective theta mapping
* Selectable combination rule
* Selectable link function \(graded response\, normal\, generalized partial credit\)
* For all of these model types\, number of parameters grows linearly with number of parents
# Noisy-And (Or)
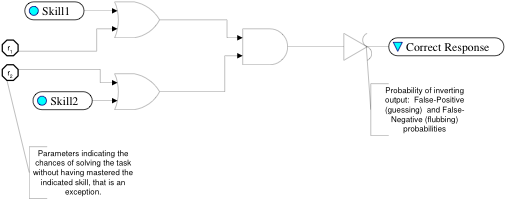
All input skills needed to solve problem
Bypass parameter for Skill _j_ \, _q_ _j_
Slip probability \(overall\)\, _q_ _0_
Probability of correct outcome
NIDA/DINA
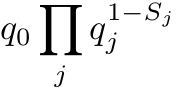
# Noisy Min (Max)
* If skills have more than two levels
* Use a cut point to make skill binary \(e\.g\.\, reading skill must be greater than X\)
* Use a Noisy\-min model
* Probability of success is determined by the weakest skill
* Noisy\-And/Min common in ed\. measurement\, Noisy\-Or/Max common in diagnosis
* Number of parameters is linear in number of parents/states
* Variants of propagation algorithm take advantage of extra Noisy\-Or/And independence conditions
# Discrete IRT (2PL) model
* Imagine a case with a single parent and a binary \(correct/incorrect\) child\.
* Map states of parent variable onto a continuous scale: _effective theta\, _
* Plug into IRT equation to get conditional probability of “correct”
* _a_ _j_ _ – _ discrimination parameter
* _b_ _j_ _ – _ difficulty parameter
* _1\.7 – _ Scaling constant \(makes logistic curve look like normal ogive\)
# DiBello--Samejima Models
Single parent version
Map each level of parent state to “effective theta” on IRT \(N\(0\,1\)\) scale\,
Now plug into Samejima graded response model to get probability of outcome
Uses standard IRT parameters\, “difficulty” and “discrimination”
DiBello\-\-Normal model uses regression model rather than graded response
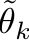
# Various Combination Rules
* For Multiple Parents\, assign each parent _j _ an effective theta at each level _k_ \, \.
* Combine Using a Combination Rule \(Structure Function\)
* Possible Structure Functions:
* Compensatory = average
* Conjunctive = min
* Disjunctive = max
* Inhibitor; e\.g\. level _k_ \* on :
* where is some low value\.
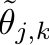

# Effective Thetas for �Compensatory Relationship
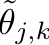
equally spaced normal quantiles
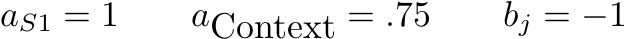
# Effective Theta to CPT
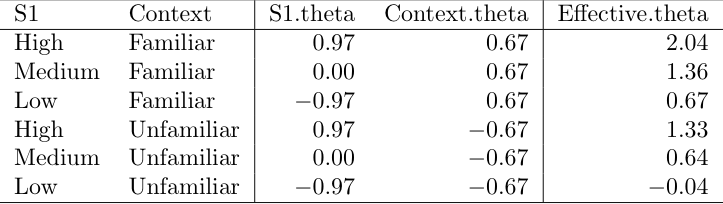
Introduce new parameter _d_ _inc_ _ _ as spread between difficulties in Samejima model
_b_ _i\,Full_ _ = b_ _j_ _ \+ d_ _inc_ _/2 b_ _j\,Partial_ _ = b_ _j_ _ \- d_ _inc_ _/2_
Conditional probability table for _ d_ _inc_ _ _ = 1 is then…
# CPTtools framework
* Building a CPT requires three steps:
* Map each parent state into a _effective theta_ for that parent
* Combine the parent effective thetas to an effective theta for each row of the CPT using one \(or more\) _combination rules_
* Combination rules generally take one or more \(often one for each parent variable\) _discrimination parameters_ which weight the parent variable contributions \(log alphas\)
* Combination rules generally take one or more _difficulty parameters_ \(often one for each state of the child variable\) which shift the average probability of a correct response \(betas\)
* Map the effect theta for each row into a conditional probability of seeing each state using a _link function_
* Link functions can take a scaling parameter\. \(link scale\)
# Parent level effective thetas
Effective theta scale is a logit scale corresponds to mean 0 SD 1 in a “standard” population\.
Want the effective theta values to be equally spaced on this scale
Want the marginal distribution implied by the effective thetas to be uniform \(unit of the combination operator\)
What the effective theta transformation to be effectively invertible \(this is reason to add the 1\.7 to the IRT equation\)\.
# Equally spaced quantiles of the normal distribution
Suppose variable has _M_ states: _0\,…\,M\-1_
Want the midpoint of the interval going from probability _m/M _ to _\(m\+1\)/M_ \.
Solution is to map state _m_ onto
R code: qnorm\(\(1:M\)\-\.5\)/M\)