

__Bayesian Networks in__ __Educational Assessment__
__Tutorial__
__Session II:__ __ __ __Bayes Net Applications __
__ __ __ACED: ECD in Action__
Duanli Yan\, Diego Zapata\, ETS
Russell Almond\, FSU
2021 NCME Tutorial: Bayesian Networks in Educational Assessment
_SESSION_ __ __ _TOPIC_ __ __ _PRESENTERS_
__Session 1__ : Evidence Centered Design Diego Zapata Bayesian Networks
__Session 2__ : Bayes Net Applications Duanli Yan & ACED: ECD in Action Russell Almond
__Session 3__ : Bayes Nets with R Russell Almond & Duanli Yan
__Session 4__ : Refining Bayes Nets with Duanli Yan & Data Russell Almond
# 1. Discrete Item Response Theory (IRT)
Proficiency Model
Task/Evidence Models
Assembly Model
Some Numbers
# IRT Proficiency Model
* There is one proficiency varaible\, __ \. \(Sometimes called an “ability parameter”\, but we reserve the term _parameter_ for quantites which are not person specific\.\)
* __ takes on values \{\-2\, \-1\, 0\, 1\, 2\} with prior probabilities of \(0\.1\, 0\.2\, 0\.4\, 0\.2\, 0\.1\) \(Triangular distribution\)\.
* Observable outcome variables are all independent given __
* Goal is to draw inferences about __
* Rank order students by __
* Classify students according to __ above or below a cut point
# IRT Task/Evidence Model
Tasks yield an work product which can be unambiguously scored _right_ / _wrong_ _\._
Each task has a _single_ observable outcome variable\.
_Tasks_ are often called _items\, _ although the common usage often blurs the distinction between the presentation of the item and the outcome variable\.
# IRT (Rasch) Evidence Model
* Let _X_ _j_ _ _ be observable outcome variable from Task _j_
* _P\(X_ _j_ _ =right | _ __ _\, _ __ _j_ _ \) _ =
* _ _ _j _ is the _difficulty_ of the item\.
* Can crank through the formula for each of the five values of __ to get values for Conditional Probability Tables \(CPT\)
# IRT Assembly Model
5 items
Increasing difficulty:
__ _ _ __ _ \{\-1\.5\, \-0\.75\, 0\, 0\.75\, 1\.5\}\. _
Adaptive presentation of items
# Conditional Probability Tables
| | Prior | Item 1 | Item 2 | Item 3 | Item 4 | Item 5 |
| :-: | :-: | :-: | :-: | :-: | :-: | :-: |
| -2 | 0.1 | 0.3775 | 0.2227 | 0.1192 | 0.0601 | 0.0293 |
| -1 | 0.2 | 0.6225 | 0.4378 | 0.2689 | 0.1480 | 0.0759 |
| 0 | 0.4 | 0.8176 | 0.6792 | 0.5000 | 0.3208 | 0.1824 |
| 1 | 0.2 | 0.9241 | 0.8520 | 0.7311 | 0.5622 | 0.3775 |
| 2 | 0.1 | 0.9707 | 0.9399 | 0.8088 | 0.7773 | 0.6225 |
# Problems Set 1
* Assume __ =1\, what is expected score \(sum _X_ _j_ \)
* Calculate _P\(_ __ _ |X_ _1_ _=_ _right_ _\)\, E\(_ __ _ |X_ _1_ _=_ _right_ _\)_
* Calculate _P\(_ __ _ |X_ _5_ _=_ _right_ _\)\, E\(_ __ _ |X_ _5_ _=_ _right_ _\)_
* Score three students who have the following observable patterns \(Tasks 1\-\-5\):
* _1\,1\,1\,0\,0_
* _1\,0\,0\,1\,1_
* _1\,1\,1\,0\,1_
5\. Suppose we have observed for a given student _X_ _2_ _=_ _right_ and _X_ _3_ _=_ _right_ \, what is the next best item to present \(hint\, look for expected probabilities closest to \.5\,\.5
6\. Same thing\, with _X_ _2_ _=_ _right_ and _X_ _3_ _=_ _wrong_
7\. Same thing\, with _X_ _2_ _=_ _wrong_ and _X_ _3_ _=_ _wrong_
# 2. “Context” effect --Testlets
* Standard assumption of conditional independence of observable variables given Proficiency Variables
* Violation
* Shared stimulus
* Context
* Special knowledge
* Shared Work Product
* Sequential dependencies
* Scoring Dependencies \(Multi\-step problem\)
* Testlets \(Wainer & Kiely\, 1987\)
* Violation results in overestimating the evidential value of observables for Proficiency Variables
# “Context” effect -- Variables
* Context variable – A parent variable introduced to handle conditional dependence among observables \(testlet\)
* Consistent with Stout’s \(1987\) ‘essential n\-dimensionality’
* Wang\, Bradlow & Wainer \(2001\) SCORIGHT program for IRT
* Patz & Junker \(1999\) model for multiple ratings
# “Context” effect -- example
Suppose that Items 3 and 4 share common presentation material
Example: a word problem about “Yacht racing” might use nautical jargon like “leeward” and “tacking”
People familiar with the content area would have an advantage over people unfamiliar with the content area\.
Would never use this example in practice because of DIF \(Differential Item Functioning\)
# Adding a context variable
Group Items 3 and 4 into a single task with two observed outcome variables
Add a person\-specific\, task\-specific latent variable called “context” with values _familiar_ and _unfamiliar_
Estimates of will “integrate out” the context effect
Can use as a mathematical trick to force dependencies between observables\.
# IRT Model with Context Variable
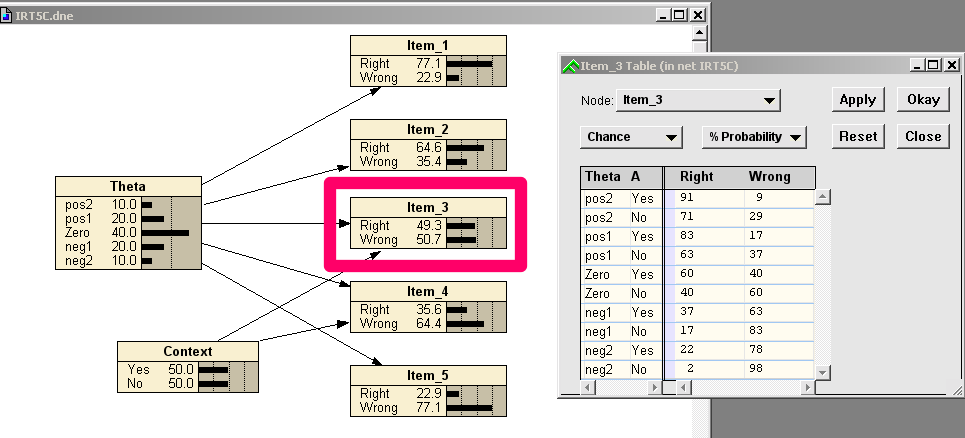
# Problem Set 2
* Compare the following quantities in the context and no context models:
* P\(X2\)\, P\(X3\)\, P\(X4\)
* P\(|X2= _right_ \)\, P\(|X3= _right_ \)
* P\(X4|X2= _right_ \)\, P\(X4 |X3= _right_ \)
* P\(|X3= _wrong_ \, X4= _wrong_ \)\, P\(|X3= _right_ \, X4= _wrong_ \)\,
* P\(|X3= _wrong_ \, X4= _right_ \)\, P\(|X3= _right_ \, X4= _right_ \)
# Context Effect Postscript
If Context effect is generally construct\-irrelevant variance\, if correlated with group membership this is bad \(DIF\)
When calibrating using 2PL IRT model\, can get similar joint distribution for __ \, _X_ _3_ \, and _X_ _4 _ by decreasing the discrimination parameter
# 3. Combination Models
Consider a task which requires two Proficiencies:
Three different ways to combine those proficiencies:
__Compensatory__ : More of Proficiency 1 compensates for less of Proficiency 2\. Combination rule is _sum_ \.
__Conjunctive__ : Both proficiencies are needed to solve the problem\. Combination rule is _minimum\._
__Disjunctive__ : Two proficiencies represent alternative solution paths to the problem\. Combination rule is _maximum\._
# Combination Model Graphs
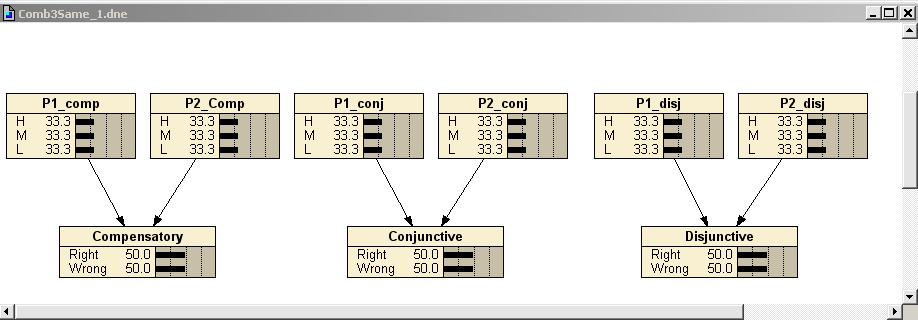
# Common Setup for All Three Models
There are two parent nodes\, and both parents are conditionally independent of each other\. The difference among the three models lies in the third term below:
_ P_ \( _P_ _1_ _\, P_ _2_ _\, X_ \) = _P_ \( _P_ _1 _ \) • _P_ \( _P_ _2 _ \) • _P_ \( _X_ _ _ _| P_ _1_ _\, P_ _2_ \)
The priors for the parent nodes are the same for the three models with 0\.3333 of probability at each of the H\, M\, and L states\.
The initial marginal probability for X is the same for the three models \(50/50\)\.
# Conditional Probability Tables
This table contains the conditional probabilities for the parent nodes \(P1 and P2\) and the combination model for the three models\.
Table 3 – Part 2
Conditional Problems for Compensatory\, Conjunctive\, and Disjunctive
_P1_ _ P2_ _Compensatory_ _Conjunctive_ _Disjunctive_ “Right” “Right” “Right”
H H 0\.9 0\.9 0\.7
H M 0\.7 0\.7 0\.7
H L 0\.5 0\.3 0\.7
M H 0\.7 0\.7 0\.7
M M 0\.5 0\.7 0\.3
M L 0\.3 0\.3 0\.3
L H 0\.5 0\.3 0\.7
L M 0\.3 0\.3 0\.3
L L 0\.1 0\.3 0\.1
# Problem Set 3
Verify that _P\(P_ _1_ _\)\, P\(P_ _2_ _\)\,_ and _P\(Obs\)_ are the same for all three models\. \( _Obs_ represents either the node _Compensatory_ \, _Conjunctive\,_ or _Disjunctive_ \)
Assume _Obs_ = _right_ \, Calculate _P\(P_ _1_ _\)_ and _P\(P_ _2_ _\)_ for all three models\.
Assume _Obs_ = _wrong_ \, Calculate _P\(P_ _1_ _\)_ and _P\(P_ _2_ _\)_ for all three models\.
Assume _Obs_ = _right_ \, and _P_ _1_ _ = _ _H_ \. Calculate _P\(P_ _2_ _\)_ for all three models\.
Assume _Obs_ = _right_ \, and _P_ _1_ _ = _ _M_ \. Calculate _P\(P_ _2_ _\)_ for all three models\.
Assume _Obs_ = _right_ \, and _P_ _1_ _ = _ _L_ \. Calculate _P\(P_ _2_ _\)_ for all three models\.
Explain the differences
# Activity 3
* Go back to the Driver’s License Exam you built in Session I and add some numbers
* Now put in some observed outcomes
* How did the probabilities change?
* Is that about what you expected?
# ACED Background
* ACED \(Adaptive Content with Evidence\-based Diagnosis\)
* Val Shute \(PD\)\, Aurora Graf\, Jody Underwood\, Eric Hansen\, Peggy Redman\, Russell Almond\, Larry Casey\, Waverly Hester\, Steve Landau\, Diego Zapata
* Domain: Middle School Math\, Sequences
* Project Goals:
* Adaptive Task Selection
* Diagnostic Feedback
* Accessibility
# ACED Features
__Valid Assessment__ \. Based on evidence\-centered design \(ECD\)\.
__Adaptive Sequencing__ \. Tasks presented in line with an adaptive algorithm\.
__Diagnostic Feedback__ \. Feedback is immediate and addresses common errors and misconceptions\.
__Aligned__ \. Assessments aligned with \(a\) state and national standards and \(b\) curricula in current textbooks\.
# ACED Proficiency Model

# Typical Task
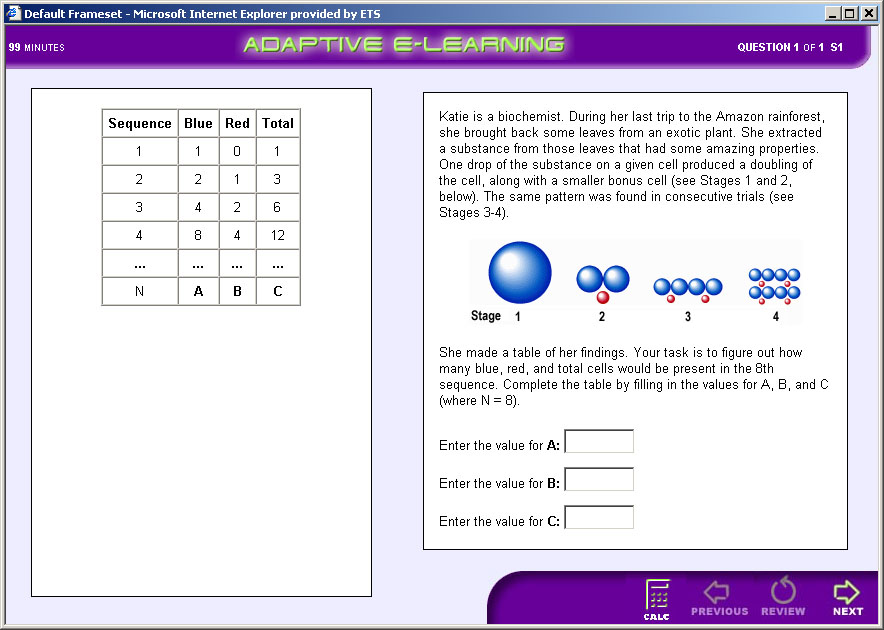
# ACED Design/Build Process
Identify Proficiency variables
Structure Proficiency Model
Elicit Proficiency Model Parameters
Construct Tasks to target proficiencies at Low/Medium/High difficulty
Build Evidence Models based on difficulty/Q\-Matrix
# Parameterization of Network
* Proficiency Model:
* Based on Regression model of child given parent
* SME provided correlation and intercept
* SME has low confidence in numeric values
* Evidence Model Fragment
* Tasks Scored _Right_ / _Wrong_
* Based on IRT model
* _High_ / _Medium_ / _Low_ corresponds to = \+1/0/\-1
* Easy/Medium/Hard corresponds to difficulty \-1/0/\+1
* Discrimination of 1
* Used Q\-Matrix to determine which node is parent
# PM-EM Algorithm for Scoring
* Master Bayes net with just proficiency model\(PM\)
* Database of Bayes net fragments corresponding to evidence models \(EMs\)\, indexed by task ID
* To score a task:
* Find EM fragment corresponding to task
* Join EM fragment to PM
* Enter Evidence
* Absorb evidence from EM fragment into network
* Detach EM fragment
# An Example

Five proficiency variables
Three tasks\, with observables \{X11\}\, \{X21\, X22 \, X23\}\, \{X31\}\.
# Q: Which observables depend on which proficiency variables?�A: See the Q-matrix (Fischer, Tatsuoka).
| | q1 | q2 | q3 | q4 | q5 | X23 |
| :-: | :-: | :-: | :-: | :-: | :-: | :-: |
| X11 | 1 | 0 | 0 | 0 | 0 | -- |
| X21 | 0 | 1 | 0 | 0 | 0 | 1 |
| X22 | 0 | 1 | 0 | 1 | 0 | 1 |
| X23 | 0 | 0 | 0 | 0 | 0 | N/A |
| X31 | 0 | 1 | 1 | 1 | 0 | -- |
# Proficiency Model / Evidence Model Split
* Full Bayes net for proficiency model and observables for all tasks can be decomposed into fragments\.
* Proficiency model fragment\(s\) \(PMFs\) contain proficiency variables\.
* An evidence model fragment \(EMF\) for each task\.
* EMF contains observables for that task and all proficiency variables that are parents of any of them\.
* Presumes observables are conditionally independent between tasks\, but can be dependent within tasks\.
* Allows for adaptively selecting tasks\, docking EMF to PMF\, and updating PMF on the fly\.
# On the way to PMF and EMFs…

Proficiency variables
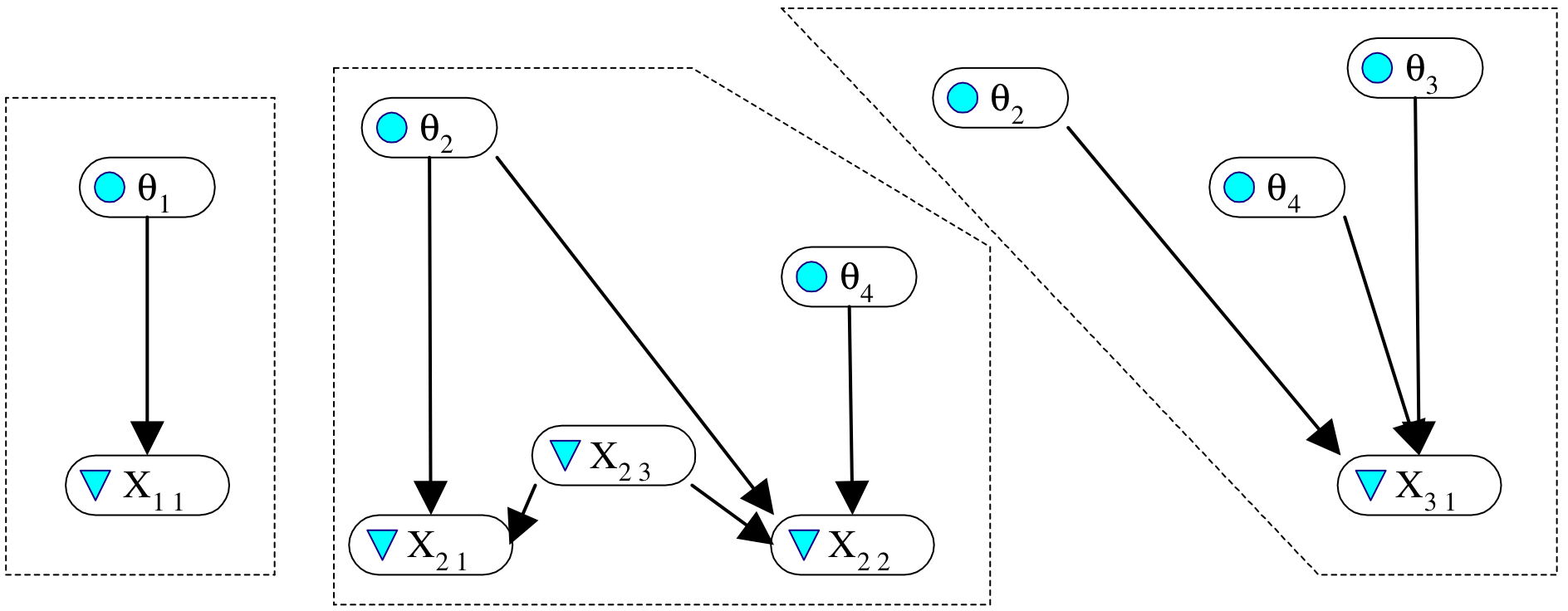
Observables and proficiency variable parents for the tasks
# Marry parents, drop directions, and triangulate (in PMF, with respect to all tasks)


# Footprints of tasks in proficiency model (figure out from rows in Q-matrix)


# Result:
* Each EMF implies a join tree for Bayes net propagation\.
* Initial distributions for proficiency variables are uniform\.
* The footprint of the PM in the EMF is a clique intersection between that EMF and the PMF\.
* Can “dock” EMFs with PMF one\-at\-a\-time\, to …
* absorb evidence from values of observables to that task as updated probabilities for proficiency variables\, and
* predict responses in new tasks\, to evaluate potential evidentiary value of administering it\.
# Docking evidence model fragments
# Scoring Exercise
| Outcome | Task Name | Proficiency Variable | Difficulty |
| :-: | :-: | :-: | :-: |
| Wrong | tCommonRatio1a.xml | CommonRatio | Easy |
| Right | tCommonRatio2b.xml | CommonRatio | Medium |
| Wrong | tCommonRatio3b.xml | CommonRatio | Hard |
| Wrong | tExplicitGeometric1a.xml | ExplicitGoemetric | Easy |
| Right | tExplicitGeometric2a.xml | ExplicitGoemetric | Medium |
| Wrong | tExplicitGeometric3b.xml | ExplicitGoemetric | Hard |
| Wrong | tRecursiveRuleGeometric1a.xml | RecursiveRuleGeometric | Easy |
| Wrong | tRecursiveRuleGeometric2b.xml | RecursiveRuleGeometric | Medium |
| Wrong | tRecursiveRuleGeometric3a.xml | RecursiveRuleGeometric | Hard |
| Right | tTableExtendGeometric1a.xml | TableGeometric | Easy |
| Right | tTableExtendGeometric2b.xml | TableGeometric | Medium |
| Right | tTableExtendGeometric3a.xml | TableGeometric | Hard |
| Wrong | tVerbalRuleExtendModelGeometric1a.xml | VerbalRuleGeometric | Easy |
| Wrong | tVerbalRuleExtendModelGeometric1b.xml | VerbalRuleGeometric | Easy |
| Right | tVerbalRuleExtendModelGeometric2a.xml | VerbalRuleGeometric | Medium |
| Wrong | tVisualExtendGeometric1a.xml | VisualGeometric | Easy |
| Wrong | tVisualExtendGeometric2a.xml | VisualGeometric | Medium |
| Wrong | tVisualExtendGeometric3a.xml | VisualGeometric | Hard |
# Weight of Evidence
Good \(1985\)
_H_ is binary hypothesis\, e\.g\.\, _Proficiency_ > _Medium_
_E_ is evidence for hypothesis
Weight of Evidence \(WOE\) is

# Properties of WOE
“Centibans” \(log base 10\, multiply by 100\)
Positive for evidence supporting hypothesis\, negative for evidence refuting hypothesis
Movement in tails of distribution as important as movement near center
Bayes theorem using log odds
# Conditional Weight of Evidence
Can define Conditional Weight of Evidence
Nice Additive properties
Order sensitive
WOE Balance Sheet \(Madigan\, Mosurski & Almond\, 1997\)
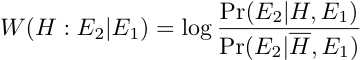

# Evidence Balance Sheet
63 tasks total
1 Easy
2 Medium
3 Hard
a Item type
b Isomorph
__P\(Solve Geom Sequences\)__
| Task | Acc | H | M | L |
| :-: | :-: | :-: | :-: | :-: |
| SolveGeometricProblems2a | 0 | 0.16 | 0.26 | 0.58 |
| SolveGeometricProblems3a | 1 | 0.35 | 0.35 | 0.30 |
| SolveGeometricProblems3b | 1 | 0.64 | 0.29 | 0.07 |
| SolveGeometricProblems2b | 1 | 0.83 | 0.16 | 0.01 |
| VisualExtendTable2a | 1 | 0.89 | 0.10 | 0.01 |
| SolveGeometricProblems1a | 0 | 0.78 | 0.21 | 0.01 |
| SolveGeometricProblems1b | 1 | 0.82 | 0.18 | 0.00 |
| VisualExtendVerbalRule2a | 1 | 0.85 | 0.15 | 0.00 |
| ModelExtendTableGeometric3a | 1 | 0.90 | 0.10 | 0.00 |
| ExamplesGeometric2a | 0 | 0.87 | 0.13 | 0.00 |
| VisualExplicitVerbalRule3a | 1 | 0.91 | 0.09 | 0.00 |
| VerbalRuleModelGeometric3a | 1 | 0.95 | 0.05 | 0.00 |
__WOE for H vs\. M\, L__
# Expected Weight of Evidence
When choosing next “test” \(task/item\) look at expected value of WOE where expectation is taken wrt _P\(E|H\)_ \.
where represent the possible results\.
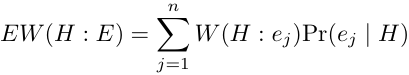
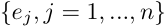
# Calculating EWOE
Madigan and Almond \(1996\)
Enter any observed evidence into net
Instantiate Hypothesis = True \(may need to use virtual evidence if hypothesis is compound\)
Calculate for each candidate item
Instantiate Hypothesis = False
Calculate for each candidate item
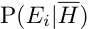
# Related Measures
Value of Information
__S__ is proficiency state
_d_ is decision
_u_ is utility
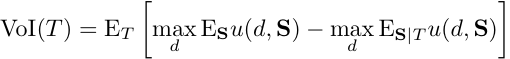
# Related Measures (2)
Mutual Information
Extends to non\-binary hypothesis nodes
Kullback\-Liebler distance between joint distribution and independence
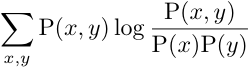
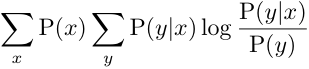
# Task Selection Exercise 1
* Use ACEDMotif1\.dne
* Easy\, Medium\, and Hard tasks for Common Ratio and Visual Geometric
* Use Hypothesis _SolveGeometricProblems_ > _Medium_
* Calculate EWOE for six observables
* Assume candidate gets first item right and repeat
Next assume candidate gets first item wrong and repeat
Repeat exercise using hypothesis _SolveGeometricProblems_ > _Low_
Use Network ACEDMotif2\.dne
Select the _SolveGeometricProblems_ node
Run the program Network>Sensitivity to Findings
This will list the Mutual information for all nodes
Select the observable with the highest mutual information as the first task
Use this to process a person who gets every task right
Use this to process a person who gets every task wrong
# ACED Evaluation
* Middle School Students
* Did not normally study geometric series
* Four conditions:
* Elaborated Feedback/Adaptive \(E/A; n=71\)
* Simple Feedback/Adaptive \(S/A; n=75\)
* Elaborated Feedback/Linear \(E/L; n=67\)
* Control \(no instruction; n=55\)
* Students given all 61 geometric items
* Also given pretest/posttest \(25 items each\)
# ACED Scores
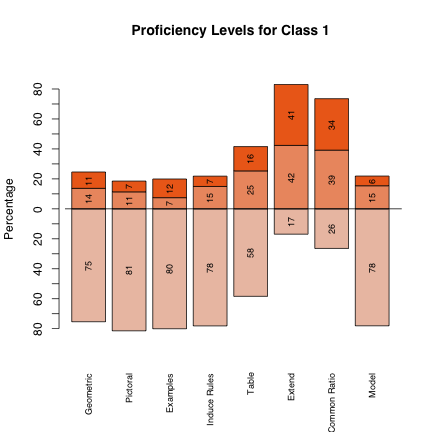
* For Each Proficiency Variable
* Marginal Distribution
* Modal Classification
* EAP Score \(High=1\, Low=\-1\)
# ACED Reliability
| Proficiency (EAP) | Reliability |
| :-: | :-: |
| Solve Geometric Sequences (SGS) | 0.88 |
| Find Common Ratio | 0.90 |
| Generate Examples | 0.92 |
| Extend Sequence | 0.86 |
| Model Sequence | 0.80 |
| Use Table | 0.82 |
| Use Pictures | 0.82 |
| Induce Rules | 0.78 |
| Number Right | 0.88 |
Calculated with Split Halves \(ECD design\)
Correlation of EAP score with posttest is 0\.65 \(close to reliability of posttest\)
Even with pretest forced into the equation\, EAP score accounted for 17% unique variance
Reliability of modal classifications was worse
# Effect of Adaptivity

For adaptive conditions\, correlation with posttest seems to hit upper limit by 20 items
Standard Error of Correlations is large
Jump in linear case related to sequence of items
# Effect of feedback
E/A showed significant gains
Others did not
Learning and assessment reliability\!\!\!\!\!
# Acknowledgements
Special thanks to Val Shute for letting us used ACED data and models in this tutorial\.
ACED development and data collection was sponsored by National Science Foundation Grant No\. 0313202\.
Complete data available at: http://ecd\.ralmond\.net/ecdwiki/ACED/ACED